Семь перпендикулярных линий красного цвета
1809 повідомлень
#14 років тому
Наверное, уже все читали рассказик про 7 перпендикулярных линий красного цвета. Кто не читал, гуглите, их валом уже перепостено в инете.А к чему тема.
Вот что-то подумалось (приснилось, что ли, что-то?), а ведь по крайней мере 7 перпендикулярных линий нарисовать реально.

Это будет всего-навсего проекция 7-мерного пространства на плоскость. Ведь 3 перпендикулярные линии все прекрасно себе представляют и даже рисовали, когда изображали куб на плоскости. Да, задачка нетривиальная, но ведь не невозможная.

Насчет линии в форме котенка и того проще - выгнуть линию, как проволоку, по контуру котенка.
Может быть, и 7 красных, из которых 3 зеленых и одна прозрачная, тоже возможно?

535 повідомлень
#14 років тому
Цитата ("raznomir2"):Может быть, и 7 красных, из которых 3 зеленых и одна прозрачная, тоже возможно?Конечно, возможно.
Рисуем в фотошопе 7 красных линий на желтом фоне. Одной линии задаем в стилях прозрачность 0%, трем другим - наложение в режиме "Исключение". В итоге, в уменьшенных превью на паннели, где отображаются слои, видим 7 красных линий, а фактически, в результате получаем 3 красных, 1 прозрачную и 3 зеленых.
Первое, что на ум пришло

1599 повідомлень
#14 років тому
Помницца, в универе наш математик строил-строил на доске с воодушевлением и искоркой в глазах десятимерные пространства, но я так ничерта и не понял. Можт после пары и понял, но потом очень быстро забыл 
В принципе, аналогию можно построить на основе двумерных человечков, живущих на двумерной поверхности глобуса (для них высота, третье измерение, никоим образом недоступна, но она существует), но у меня мозги болеть начинают ))
5629 повідомлень
#14 років тому
Цитата ("Crist"):
аналогию можно построить на основе двумерных человечков
Меня тоже чем то таким стращали

Но по моему и на одной плоскости можно нарисовать сколько угодно перпендикулярных линий если не гуглить

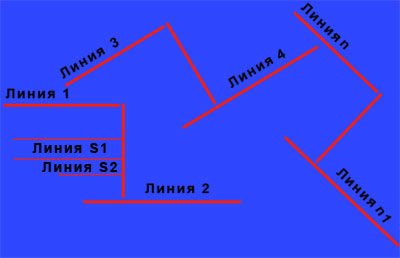
По моему суть проблемы заключается в том, что Линия 1 (см. схему) Линия S1 и Линия S2 это не одна и та же линия

А многие этого просто не понимают

Вобще же если рассматривать вариант с кубом то в трехмерном пространстве получим еще 2 перпендикулярных линии

1064 повідомлення
#14 років тому
Цитата ("raznomir2"):Ведь 3 перпендикулярные линии все прекрасно себе представляют и даже рисовали, когда изображали куб на плоскости.
Ну-ну... нарисуйте хоть три, я посмотрю.
6970 повідомлень
#14 років тому
mirekua, а ничего, что на Вашем рисунке три группы параллельных линий и ещё несколько углов, отличных от 90°?
5333 повідомлення
#14 років тому
Цитата ("mirekua"):Но по моему и на одной плоскости можно нарисовать сколько угодно перпендикулярных линий если не гуглить
Нарисовать больше двух взаимоперпендекулярных линий на двухмерной плоскости невозможно, даже если сколько угодно гуглить.
Цитата ("mirekua"):
А многие этого просто не понимаютЕстественно.
Цитата ("raznomir2"):
а ведь по крайней мере 7 перпендикулярных линий нарисовать реально.Нереально. На плоскости — нереально.
Цитата ("raznomir2"):
Ведь 3 перпендикулярные линии все прекрасно себе представляютНе представляю.
Цитата ("raznomir2"):
и даже рисовали, когда изображали куб на плоскостиКуб на плоскости рисовал, но в двухмерном изображении двухмерного куба нет ни одного прямого угла, соответственно нет никаких перпендикулярных линий.
Цитата ("raznomir2"):
Насчет линии в форме котенка и того проще - выгнуть линию, как проволоку, по контуру котенка.Вы забыли, что это должна быть прямая линия.
Цитата ("raznomir2"):
Может быть, и 7 красных, из которых 3 зеленых и одна прозрачная, тоже возможно?Невозможно. В любом случае, в результате получим сколько-то три красных и три зеленых линии.
Цитата ("widder_mg"):
Ну-ну... нарисуйте хоть три, я посмотрю.Я бы тоже с удовольствием посмотрел.
Цитата ("voron_76"):
mirekua, а ничего, что на Вашем рисунке три группы параллельных линий и ещё несколько углов, отличных от 90°?Многие этого не понимают.))))))))))))
5629 повідомлень
#14 років тому
Цитата ("voron_76"):а ничего, что на Вашем рисунке три группы параллельных линий и ещё несколько углов, отличных от 90°?
Согласен. С градусом надо быть поосторожнее

А вообще то Линия 1 (см. схему) Линия S1 и Линия S2 паралельны по отношению друг к другу.
Но по отношению к не обзначенной линии они перпендикулярны

Или нет ?
 И если не вдаваться в градусы то Линия 3 и 4 например тоже перпендикулярны к необозначенной линии но паралельны по отношению друг к другу
И если не вдаваться в градусы то Линия 3 и 4 например тоже перпендикулярны к необозначенной линии но паралельны по отношению друг к другу 
Цитата ("epavlovich"):
Нарисовать больше двух взаимоперпендекулярных линий на двухмерной плоскости невозможно
Вот в чем дело оказывается.
 О взаимоперпендикулярных линиях ведь речи то не было
О взаимоперпендикулярных линиях ведь речи то не было 
5333 повідомлення
1809 повідомлень
#14 років тому
Цитата ("epavlovich"):Нарисовать больше двух взаимоперпендекулярных линий на двухмерной плоскости невозможно, даже если сколько угодно гуглить.
А где в техзадании было сказано о двумерной плоскости, а?

Цитата ("epavlovich"):
Вы забыли, что это должна быть прямая линия.
Аналогично, где в техзадании было написано, что это должна быть прямая линия? :P
5629 повідомлень
#14 років тому
Цитата ("epavlovich"):Была речь.
Я же писал - лучше не гуглить

Всегда так. Никто не хочет меня слушать

6970 повідомлень
#14 років тому
Цитата ("raznomir2"):Цитата ("epavlovich"):Нарисовать больше двух взаимоперпендекулярных линий на двухмерной плоскости невозможно, даже если сколько угодно гуглить.
А где в техзадании было сказано о двумерной плоскости, а?
Вы можете попробовать нарисовать семь перпендикулярных линий в семимерном пространстве. А мы потом поздравим Вас с нобелевкой.
1809 повідомлень
#14 років тому
Цитата ("voron_76"):Вы можете попробовать нарисовать семь перпендикулярных линий в семимерном пространстве.
Я этого не умею.
Но утверждать, что это невозможно - получается, уже неправильно.
Элементарно, можно ответить в стиле: "да, это возможно, но нужно для этого семимерное пространство, как только заказчик предоставит требуемое, так и нарисую".
5333 повідомлення
#14 років тому
Цитата ("raznomir2"):где в техзадании было написано, что это должна быть прямая линия?Если я не ошибаюсь (а я в данном случае не ошибаюсь), то понятие «перпендикулярность» оперирует либо плоскостями, либо векторами, либо прямыми. Кривые линии и поверхности не могут пересечься под прямым углом.
Цитата ("mirekua"):
Я же писал - лучше не гуглитьВ данном случае нужно гуглить, хотя бы для того, чтобы знать условие задачи.
Всегда так. Никто не хочет меня слушать
1809 повідомлень
#14 років тому
Цитата ("epavlovich"):Если я не ошибаюсь (а я в данном случае не ошибаюсь), то понятие «перпендикулярность» оперирует либо плоскостями, либо векторами, либо прямыми. Кривые линии и поверхности не могут пересечься под прямым углом.
В конце концов того же котенка можно нарисовать краснозелеными цветами на линии, толщина линий не оговаривалась, вроде бы.
Котенок формулировался как "в виде котенка". Как вариант, края вырезать по контуру котенка.
С рассказом интересно получилось. Читатели автоматически взяли стандартные ограничения (двухмерная плоскость, линия как математическое понятие без толщины, цвет строго плоского понятия, а не как составной), и радостно поржали над идиотами-заказчиками.
Собственно, как и в реальной жизни.

А заказчик мог элементарно подразумевать что-то другое. С учетом же идиотизма менеджеров-посредников, получили то, что получили.
Т.е. не все так однозначно в рассказе, если посмотреть на ситуацию с другой стороны. :P
6970 повідомлень
#14 років тому
Цитата ("raznomir2"):Элементарно, можно ответить в стиле: "да, это возможно, но нужно для этого семимерное пространство, как только заказчик предоставит требуемое, так и нарисую".
Бумагу-краски-фотошопы Вам тоже заказчик предоставляет?
Цитата ("raznomir2"):
Т.е. не все так однозначно в рассказе, если посмотреть на ситуацию с другой стороны.
Может, Вы просто реализуете это задание, покажете здесь и посмеётесь над идиотами-читателями?
1064 повідомлення
#14 років тому
Цитата ("raznomir2"):А где в техзадании было сказано о двумерной плоскости, а?
А Вы на чём ещё рисовать умеете?
Цитата ("raznomir2"):
Аналогично, где в техзадании было написано, что это должна быть прямая линия?
Непрямая перпендикулярная линия не на плоскости - это реально круто. Присоединяюсь к очереди жаждущих поздравить с Нобелевской премией

1809 повідомлень
#14 років тому
Я в восторге от силы желания остаться правым, лишь бы не выходить за рамки собственных представлений о мире.Браво, так и продолжайте,

P.S. Знаете, был случай из практики. Когда мы дали ТЗ профессиональному дизайнеру, а он сначала согласился и начал работать, но потом после длительного процесса попыток нарисовать вдруг заявил, что это невозможно, ибо в ТЗ есть противоречия. Дело закончилось тем, что точно это же ТЗ без каких-либо добавлений отдали другому дизайнеру, менее крутому. И через пару дней с первой же попытки получили именно то, что и хотели, в полном соответствии ТЗ, и никаких особенных сложностей это почему-то у нового исполнителя не вызвало.
Может, все-таки что-то в консерватории не то?








