Полночная загадка

Цитата ("dervinar"):

Но внимание вопрос - а как же тогда Архимед вывел Пи? Он тоже делает какой то многоугольник, который похож на круг, и говорит, что при n->бесконечности периметр этого многоугольника приравняется кругу...

Архимед исходил из того, что среднее значение площадей описанного и вписанного многоугольников с одинаковым количеством сторон стремится к площади круга (и это предположение верное).
Аналогично, среднее значение периметров описанного и вписанного многоугольников стремится к длине окружности.

Кстати, для вычисления площади круга Архимед использовал не квадраты или прямоугольники, а правильные многоугольники с большим количеством углов. Начал с шестиугольника, описывающего окружность, потом удваивал количество сторон вплоть до получения 96-угольника. Посчитал площадь этого 96-угольника. Повторил то же самое для вписанного многоугольника. Взял среднее значение площадей, получил приблизительную площадь круга. Потом, обнаружив квадратичную зависимость площади круга от радиуса, он вывел приближенное значение числа Пи, что позволило ему вычислять площади любых кругов, зная их радиус. Подобным же методом он и длину окружности определял.

Цитата ("hiberok"):

Ошибка в пункте 5, в котором обозначено, что все точки полученного много-многоугольника лежат на окружности, а по сути часть из них всегда будет лежать ВНЕ окружности, отсюда и неравенство периметра и длины окружности.

Да, абсолютно правильно.
Именно поэтому метод, описанный в первом посте на картинке, для определения длины окружности вообще не применим.
Зато этот метод применим для вычисления площади круга, из которой в свою очередь тоже можно получить приближенное значение Пи. Только это более трудоемко, и менее точно, чем с многоугольниками (возможно, поэтому Архимед и выбрал решение с многоугольниками).

Как бы вы друзья ни выкручивались, но притянуть зауши заданную в условии топика куски линейной функции к нелинейной (окружность) не удастся. Катеты по-любому останутся катетами и ни куда от этого ни деться. А Архимед хоть древний дядька был, но гений, он еще и расчитал расстояние от Земли до Солнца. А после него через пятьсот лет или 600 (не важно) таких как он на кострах жгли и думали, что Земля плоская.

Цитата ("k-a-j"):

А Архимед хоть древний дядька был, но гений, он еще и расчитал расстояние от Земли до Солнца.

Вроде не Архимед, а Аристарх. Архимед писал об измерении расстояния от Земли до Солнца, пересказывая Аристарха, и ссылаясь на него.

Насколько я вижу, правильный ответ уже звучал неоднократно, как-то ТС не реагирует, упираясь в то, что вырезания таких кубиков приведет к тому, что они будут походить на дугу.
Явно же это не так. Рельефность, вот она и дает четверку для значения Пи. просто не правильный метод.
Метод равностороннего (tvv говорит правильного, не знаю, наврное так правильнее будет сказать ) многоуголника тем лучше, что при увеличении количеств сторон, увеличиваеться угол между сторонами и изменяеться общий периметр многоуголника!

MrWolf, там рассказывали о правильном многоугольнике описывающем окружность. При стремлении длины сторон к нулю периметр многоугольника будет стремиться к длине окружности. Но в топике случай с вырезанием прямоугольников, т.е. угол 90 градусов всегда, независимо от количества итераций. По-этому мы с вами и твердим о неизменности периметра, он как был 4d так и останется.

Цитата ("tvv"):

Вроде не Архимед, а Аристарх. Архимед писал об измерении расстояния от Земли до Солнца, пересказывая Аристарха, и ссылаясь на него.

Как говорят украинцы "не знав, не знав та й забув", так и я. Туман в голове, но тем не менее Архимед дядька гениальный.

Цитата ("tvv"):

все стороны между собой равны и все углы между собой равны

Это я и имел ввиду Значит "правильный" )))

Четырехугольники с окружностями хитрые, сами имеют по 4d градусов, а как только в окружность вписывается другая фигура с тремя углами или больше четырех, так все, дружба заканчивается. Но при этом чем больше градусов, тем периметр ближе к длине окружности и естественно площади. Точно как человек, при большом количестве градусов к земле тянется, так в ней и хочет раствориться. Вывод: человек - периметр Земли.

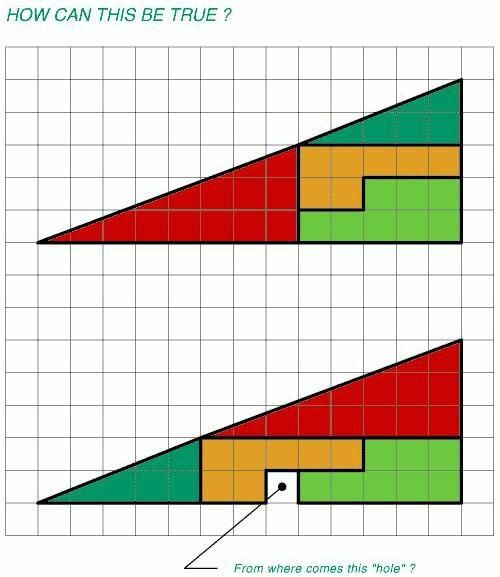
Когда были частично правильные ответы - я об этом говорил.
Много людей высказывали, вообще говоря, правильные вещи, но они не являлись ответами на поставленный вопрос.
Еще кое кто высказывал столь категоричные утверждения, что если им следовать - и Архимед тоже не имел никакого права считать Пи=)

Правильный же ответ звучит так - в момент перехода от 4 к 5 можно однозначно заключить только что на бесконечности P(периметр круга)<=4.
И если мы хотим дать какой то более полный ответ, мы должны ограничить Пи с внутренней стороны, и вывести неравенство вида P>=x. Как это, собственно, и сделал Архимед.

Если вы вспомним мой первый пост - я там прямо написал, что награду получает не первый правильный ответ, а правильный, и при этом доступно для обывателей объясняющий парадокс.
Итого - мое имхо, тут никто не заслужил награды.
Чтобы меня не обвиняли в зажиливании 5$ - вот вам еще одна загадка, тут ответ может быть только один, и он крайне прост и однозначен. Первый отгадавший получает 5$ сразу.

Собственно вопрос - откуда взялось пустое место, или куда делся 1 квадратик?

dervinar, интересно с треугольниками. Пока ответ не знаю. Но если посмотреть, то например если приложить по сетке зеленый треугольник поверх красного, то острие попадает вровень с вертикалью на точку "From". Но не на угол сетки как на верхнем рисунке.

Цитата ("k-a-j"):

dervinar, интересно с треугольниками

Ответ простой. Это не треугольники

Цитата ("oren"):

Цитата ("k-a-j"):

dervinar, интересно с треугольниками

Ответ простой. Это не треугольники

Да. Нижний- четырехугольник.

Верхний - тоже четырёхугольник

Цитата ("dervinar"):

Правильный же ответ звучит так - в момент перехода от 4 к 5 можно однозначно заключить только что на бесконечности P(периметр круга)<=4.
И если мы хотим дать какой то более полный ответ, мы должны ограничить Пи с внутренней стороны, и вывести неравенство вида P>=x. Как это, собственно, и сделал Архимед.

Если вы вспомним мой первый пост - я там прямо написал, что награду получает не первый правильный ответ, а правильный, и при этом доступно для обывателей объясняющий парадокс.
Итого - мое имхо, тут никто не заслужил награды.

Ограничить только лишь с внутренней стороны недостаточно. Нужно ограничить и с внешней, и с внутренней, и получить среднее значение.

Но в любом случае, прошу прощения, Вы действительно читали мое сообщение, которое я написал вчера в 21:41?

Архимед считал ПЛОЩАДЬ КРУГА путем нахождения площадей _описанного_ и _вписанного_ МНОГОУГОЛЬНИКОВ и последующего определения _среднего значения_ этих площадей. Примерное значение числа Пи (точнее, диапазон, куда оно входит) он вывел, найдя квадратичную зависимость площади круга от радиуса. Уже потом он стал выводить длину окружности. Это — общеизвестный факт.

А Вы можете ли пожалуйста дать хоть какую-то ссылку, подтверждающую, что то объяснение (да и сама задача с квадратом тоже), которое Вы привели в первом посте, имеет хоть какое-то отношение к Архимеду?

dervinar, на последнем рисунке верхняя линия не прямая. В первом случае она вогнута вниз, во втором - выгнута вверх. Вот и разница в площади. А еще выходит, что oren прав. Это не треугольники

Цитата ("oren"):

Ответ простой. Это не треугольники

Да, все правильно. Это не треугольники, так как одна из сторон (соответствующая гипотенузе, если бы это были бы треугольники) не лежит на прямой. У одной фигуры она немного вогнутая, у другой — немного выпуклая, разница между площадями этих фигур и составляет как раз площать того "потерянного" квадрата. Детский сад.

Цитата ("tvv"):

Детский сад

))

Цитата ("dervinar"):

На расстояние от окружности до каждой точки с каждой последующей итерацией все уменьшается и уменьшается, и стремится к нулю при колличестве итераций, стремящемся к бесконечности.

Это абсолютно не важно.
Порок Вашего примера не в том, где лежат точки относительно вписанной окружности, а в том, что в Вашей фигуре периметр не зависит от количества изломов и граней. Он есть константа и не может быть использован сравненения со вписанной окружностью.
А в описанном или вписаном выпуклом многоугольнике периметр есть функция от количества граней и при стремлении количества граней к бесконечности его периметр будет стремиться к длинне окружности.

ЗЫ Если не ошибаюсь, есть метод вычисления площади круга с помощью фигуры, подобной Вашей. Только она должна быть вписанной. Тогда при увеличении числа изломов меняется высота и ширина фигуры и ее периметр и площадь становятся функцией количества изломов.