Полночная загадка

Прислали тут мне ссылку на неплохую загадку, в духе Ахиллеса и черепахи. Собственно, укажите на ошибку в рассуждениях.
Денег за разгадку не пообещаю - наверняка тинай найдет много совпадений, возможно, что и портал с моим ответом найдет, если успеет к тому времени проиндексировать. Да и загадка простейшая, вообще говоря, любой программист с аналитическим складом ума должен такое решить.
Но за самый оригинальный и доступный для поверхностно знакомых с геометрией и логикой ответ выдам приз, минимум в 5$.

Да, если вдруг кто настолько не знаком с английским языком, перевожу надписи.
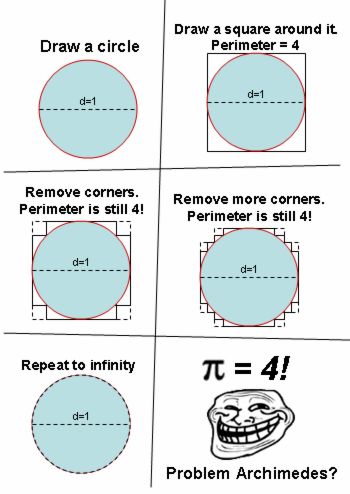
1) Рисуем круг, с диаметром, равным 1.
2) Рисуем квадрат, описанный вокруг круга. Периметр квадрата, как несложно подсчитать = 4.
3) Отрезаем угол. Как видно из построения, периметр не изменился - тоесть по прежнему равен 4.
4) Продолжаем отрезать углы... Как видно из построения, периметр по прежнему не меняется и равен 4.
5) Продолжаем до бесконечности отрезать углы.
6) Таким образом, получаем, что число пи (отношение периметра круга к его диаметру) равняется 4.
Если кто то так и не понял, а в чем тут проблема, напоминаю, что число пи почему-то всегда считают равным 3,14 и дальше еще много цифр после запятой, но никак не 4.

dervinar, зачем делать remove corners? насколько я знаю, то там вычисляли Пи с помощью равностороннего многоугольника.
Да и переход с четвортого на пятый, помоему поспешный. Там дальше кубик убрать не получиться , а придеться иметь дело с дугой.. вот как раз они и дают знаечение, меньше, чем 4, тоесть 3,14 )))

Что, нет? Опозорился? Или Вы интригу держите? )

Это я вот грубо проиллюстрировал почему так не пойдет.

Думаю в таком варианте (масштабе) видно, что получаеться почти прямоугольный треугольник и два катета по-любому больше гипотенузы (хоть и не совсем ровной )

Теперь я уверен, что я прав :P

Я спать, хоть тему не удаляйте до утра

Просто не думал, что кто-то на это будет отвечать в 3 ночи, сорри=)
MrWolf, вы безусловно правы, в том что где-то в этих рассуждениях имеется ошибка. Еще бы ей не иметься, если пи все таки ~ 3.14 и никак не 4.
И да, безусловно, Архимед действовал через увеличение углов у многоугольников, и разумеется, если повторить его опыт, мы придем к ~ 3.14.
Все это замечательно, но никоим образом не отвечает на вопрос, где же все-таки закралась ошибка.

Переход с 4 на 5 картинку поспешен? Чем? Дуга тут ни при чем - я просто отрезаю уголки от своей фигуры, делая её более похожей на круг.
Кубик(вообще говоря, квадратик) я и на 4 картинке не убираю - я каждый раз отрезаю прямоугольники от угла, выбирая прямоугольник, который будет касаться круга. За счет того, что я отрезаю прямоугольник, периметр сохраняется неизменным (насколько помним из 5-6-го урока по геометрии, в прямоугольнике противолежащие стороны равны). А с каждой итерацией полученная фигура все ближе и ближе приближается к кругу. Сделаю 100 картинок - вы на таком разрешении уже не заметите разницы, а мы говорим о бесконечности.

"Доказательство" из последующего поста вообще не доказывает ничего.
"Видно" это не доказательство, это раз.
Два - треугольники кривые и круга не касаются, но это я придираюсь=)
Три - если следовать вашей логике (вообще говоря то, что сумма двух сторон треугольника в случае, если он не вырожден всегда больше, чем третья сторона верно для любых треугольников, а не только для прямоугольных) получается что Архимед тоже нифига не прав был.

Ладно, если серьезно, то вы высказали в общем правильное утверждение(если нарисовать более аккуратно), действительно в данном случае длина дуги будет больше, чем сумма "катетов" (хотя бы просто потому, что пи в нашем мире равен 3,14 а не 4), но ДОКАЗАТЬ это, не зная заранее правильного пи невозможно. Ну не существует иного способа посчитать длину дуги, а "как мы видим" - это все таки не может служить доказательством, да еще и с таким количеством оговорок("почти прямоугольные треугольники", "гипотенуза, хоть и не ровная". А для другого треугольника и другой "не ровной гипотенузы" ваше утверждение уже будет неверно.

И еще раз обращаю ваше внимание. Мне не нужно доказывать, что длина дуги будет меньше, чем периметр ограничивающей эту дугу части загигулины. Это очевидно, потому что Архимед был прав.
Обьяснить нужно именно в какой момент и в чем конкретно в рассуждениях, представленных на картинке допущена ошибка.

5 утра... почитал... моск ушел в сумрак и я пошел спать.... видимо подустал я сегодня... хотя по геометрии и начерталке было 5

Дак это древяя вешь - называется квадратура круга...

dervinar, В периметре - понятие периметр.
Ошибка в самом первом шаге, когда отрезали углы...получилась фигура, а ее периметрами не меряют.

AXAB, вы шовинист. Эта загигулина между прочим гордый невыпуклый многоугольник! И обладает всеми теми же свойствами(и правами!), в частности периметром, какими обладают и все остальные геометрические фигуры.
По сути - нет, вы не правы, периметр это не что иное, как суммарная длина границы фигуры. В случае многоугольника, в том числе и невыпуклого - сумма длин всех сторон.

dervinar, Ги Зато я знаю, что круг это геометрическое место точек, равно удаленных от центра... Помню я Ивана Ильича пятерку за это схлопотал...

Круг не станет квадратом как баба - девкой. Девка может стать бабой, а круг все равно останется кругом. Цитата ("dervinar"):

Эта загигулина между прочим гордый невыпуклый многоугольник!

Так и останется с постоянным периметром в 4-пи. А круг как бы ни пыжился, но периметр его не сможет достигнуть 3,15.
MrWolf, правильно ответил, там подмена суммы катетов на длину гипотенузы подразумевается. И математика тут не нужна.
Короче приз мистеру вольфу .

С 4 на 5 - в конечном итоге круг не получится, получится квадрат.

Да, еще. Там если продолжить вырезать квадратики, то вообще 2-d останется, крест.

k-a-j, Скажи, какая тупизна вокруг? Ну а Вольфа сколь не корми, его гипотинуза всеодно в лес затянет... по ягодицы побежит...

K-a-j, там подразумевается то, что при бесконечном колличестве итераций данная фигура стремится к кругу. Yill, квадрата там не получится, получится фигура, которая на dS->0 отличается от круга по площади.
Пока нет ни одного хотя бы правильного ответа... Печально, я думал, что будет легче.. Или может просто еще не проснулись?...

AXAB, . Не зли брат зубастого, разметелит и фамилию не спросит. Видал? Как он квадраты разметал.

k-a-j, Да он спит небось,сейчас можно пошалить...а вот ночером, я в лес ни ногой, даже с гипотенузой...

Цитата ("dervinar"):

данная фигура стремится к кругу

Это вам так хочется, что стремится к кругу. Я же вам написал, что как была она с зазубринами так и останется. Что должно произойти, чтобы зазубрины закруглились? 3 d мы получаем потому, что гнем диаметр прикладывая к кругу. Приложили трижды и тоже не сошлось. Точно так и с зазубринами будет лишнее, как бы мы молотком ни стучали.

Цитата ("AXAB"):

я в лес ни ногой, даже с гипотенузой...

Понятное дело, что с гипотенузой дома сподручнее днем и особенно ночью.

Цитата ("k-a-j"):

Цитата ("dervinar"):

данная фигура стремится к кругу

Это вам так хочется, что стремится к кругу. Я же вам написал, что как была она с зазубринами так и останется. Что должно произойти, чтобы зазубрины закруглились? 3 d мы получаем потому, что гнем диаметр прикладывая к кругу. Приложили трижды и тоже не сошлось. Точно так и с зазубринами будет лишнее, как бы мы молотком ни стучали.

А вы непосредственно процедуру вычисления пи знаете\помните? Там тоже зазубрины, и тоже при количестве итераций, стремящемся к бесконечности суммарная площадь этих "зазубрин" плавно убывает до нуля. Поэтому несмотря на то что да, действительно, при любом конечном количестве итераций зазубрины останутся, это никаким образом не обьясняет неверность полученного результата.

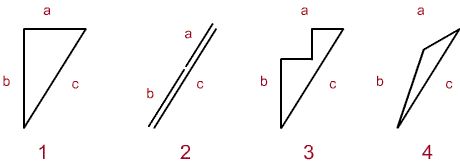
Проблема в самом принципе приближения.
Как уже говорили предыдущие ораторы, катет + катет != гипотенуза.
Возьмем прямоугольный треугольник (рис.1). У него a + b != c.
Сумма a + b будет равна с в случае если а и b будут параллельны с (рис. 2).
При вырезании угла мы не получим приближения суммы длин двух сторон к длине третьей стороны (рис. 3). Независимо от количества итераций сумма не изменится.
Приближение мы получим если будем увеличивать угол (рис. 4). А в этом случае длины сторон будут уменьшаться.

П. С. "!=" это "не равно"